蒙提霍尔问题（三门问题）诠释世界杯足球投注例子

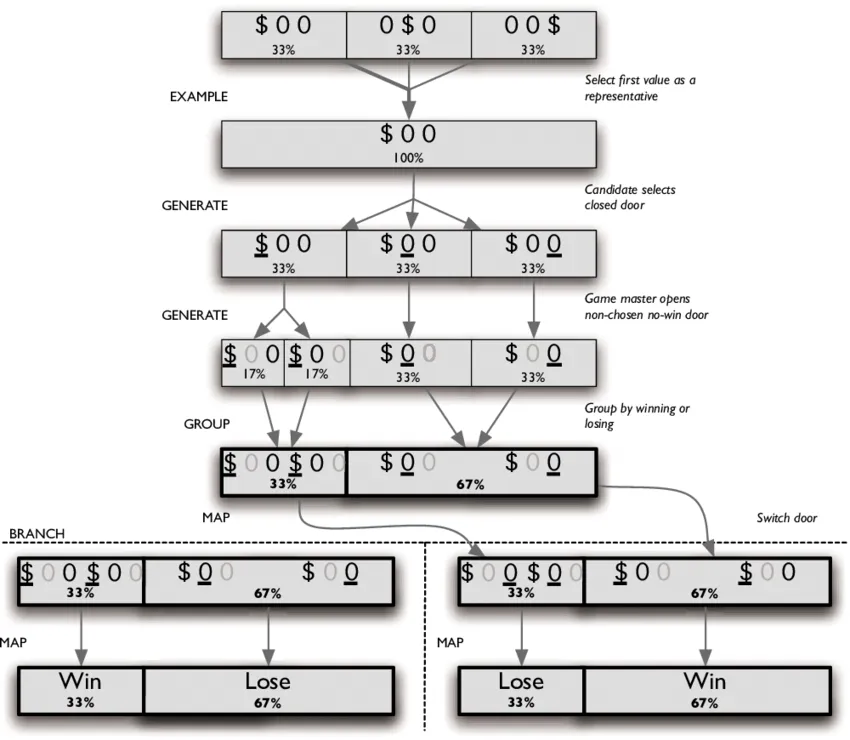
在三门问题中，主持人打开一扇无奖品的门后，换门的获胜概率为 $\\frac{2}{3}$，而坚持原选择的获胜概率为 $\\frac{1}{3}$。
这种思路可以运用到世界杯投注中，通过条件概率的分析动态调整投注策略。

情境描述

假设一场比赛，主队 (A) 对阵客队 (B)。投注者初始选择“主队胜 (A 胜)”。比赛进行过程中，外界提供了一些信息，
例如主队罚失点球、客队控球率提升等。这些信息类似于三门问题中主持人提供的额外信息。以下通过条件概率计算展示如何优化投注策略。

初始概率

设初始概率如下：

$$
P(A) = 0.4, \\quad P(B) = 0.3, \\quad P(T) = 0.3
$$

投注者选择“主队胜 (A 胜)”。

信息更新

比赛进行到第 30 分钟，主队罚失点球，客队控球率显著提升，投注平台动态调整赔率。这相当于三门问题中主持人提供的额外信息。
更新后的概率为：

$$
P(A \\mid \\text{信息}) = 0.25, \\quad P(B \\mid \\text{信息}) = 0.5, \\quad P(T \\mid \\text{信息}) = 0.25
$$

条件概率分析

根据贝叶斯公式，条件概率计算如下：

$$
P(A \\mid \\text{信息}) = \\frac{P(\\text{信息} \\mid A) \\cdot P(A)}{P(\\text{信息})}
$$

$$
P(B \\mid \\text{信息}) = \\frac{P(\\text{信息} \\mid B) \\cdot P(B)}{P(\\text{信息})}
$$

$$
P(T \\mid \\text{信息}) = \\frac{P(\\text{信息} \\mid T) \\cdot P(T)}{P(\\text{信息})}
$$

其中：
$$
P(\\text{信息}) = P(\\text{信息} \\mid A)P(A) + P(\\text{信息} \\mid B)P(B) + P(\\text{信息} \\mid T)P(T)
$$

假设与计算

假设罚失点球对主队胜的影响较大：
$P(\\text{信息} \\mid A) = 0.2$，客队控球率提升：
$P(\\text{信息} \\mid B) = 0.5$，平局影响较小：
$P(\\text{信息} \\mid T) = 0.3$。

计算 $P(\\text{信息})$：

$$
P(\\text{信息}) = 0.2 \\cdot 0.4 + 0.5 \\cdot 0.3 + 0.3 \\cdot 0.3 = 0.32
$$

更新后的条件概率：

$$
P(A \\mid \\text{信息}) = \\frac{0.2 \\cdot 0.4}{0.32} = 0.25, \\quad P(B \\mid \\text{信息}) = \\frac{0.5 \\cdot 0.3}{0.32} = 0.47, \\quad P(T \\mid \\text{信息}) = \\frac{0.3 \\cdot 0.3}{0.32} = 0.28
$$

策略调整

根据更新后的概率：

• 主队胜的概率从 $0.4$ 降至 $0.25$，胜率显著降低，可考虑更改投注。
• 客队胜的概率从 $0.3$ 提升至 $0.47$，胜率显著提高，转向投注“客队胜”可能更优。
• 平局的概率变化不大，可视赔率决定是否小额投注。

结论

通过三门问题的思路，世界杯投注中可根据信息动态调整策略。数学家的方式强调用概率和条件概率重新评估选项，而非盲目坚持初始选择。
这不仅优化了投注策略，也体现了概率理论在不确定性中的实际应用。